摘要：本文深入解析微分符号、dx与dy的含义与运用。微分符号表示函数在某一点上的微小变化量，是微积分学中的基础概念。dx和dy则分别表示自变量和函数的微小变化量，用于表示函数在某区间内的变化率。本文还将探讨这些概念在物理学、工程学、经济学等各个领域的应用，帮助读者更好地理解并运用这些重要的数学概念。

在数学的广阔天地里，我们经常会遇到一些看似简单却蕴含着深奥知识的符号，它们构成了数学世界的基石，帮助我们理解和解决复杂的问题，微分符号、dx和dy就是这样一组重要的概念，它们究竟代表了什么呢？让我们共同揭开它们的神秘面纱。

微分符号

微分符号，通常表示为“d”，在数学中扮演着至关重要的角色，微分是数学中的一个重要概念，用于描述函数局部的变化率，当我们对一个函数进行微分时，实际上是在寻找该函数在某一点附近的切线斜率，这个符号代表了微小的变化量，帮助我们量化这种变化，微分的应用广泛，不仅在数学领域，还在物理、工程、经济等领域发挥着重要作用。

dx与dy

当我们谈论微分时，经常会遇到dx和dy这两个表达式。

1、dx：dx可以看作是自变量x的微小变化量，在函数y=f(x)中，当x发生微小的改变时，会引起y的变化，这个微小的改变量就表示为dy，而dx就是描述这种变化的量，在实际应用中，dx常常用于表示某种物理量的微小变化。

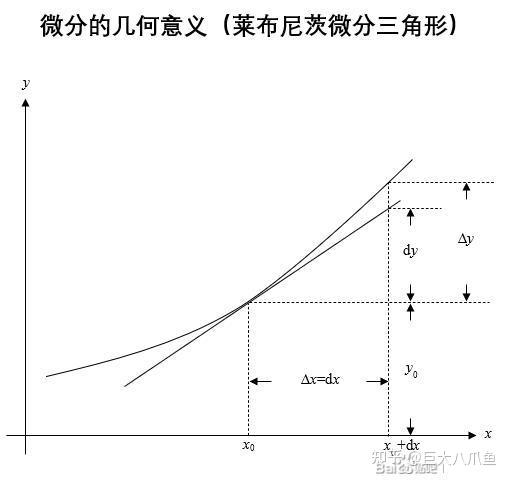
2、dy：与dx相对应，dy表示函数值y的微小变化量，当我们对函数进行微分时，dy表示函数在某一特定点的切线斜率与该点处的函数值对应的y坐标的微小变化量，在几何上，dy可以理解为切线的长度或斜率的变化量，在物理学中，dy可能代表某种物理量的瞬时变化率。

微分符号、dx与dy的含义与运用

微分符号、dx和dy是相互关联的概念。“d”代表了微小的变化量，“x”和“y”则是这种变化量在自变量和函数值上的体现，在实际应用中，我们常常需要求解函数的导数，即函数在某一点的切线斜率，这时，dx和dy就起到了重要的作用，通过求解dy/dx（即函数y关于x的导数），我们可以了解函数在某一点附近的局部行为，如增减性、极值等，dy/dx还可以帮助我们理解物理世界的各种现象，如速度、加速度、力等的变化规律。

微分符号、dx和dy是数学中的重要概念，它们帮助我们理解和解决复杂的问题，通过求解dy/dx，我们可以深入了解函数的局部行为和物理世界的各种现象，这些概念的应用广泛，涉及物理、工程、经济等多个领域，在实际学习和工作中，我们应该注重理解这些概念的本质含义和应用场景，通过实践来加深对这些概念的理解，希望本文的介绍能够帮助读者对微分符号、dx和dy有更深入的理解和认识。